Quantum Cryptography
I wrote this summary of quantum cryptography for a research project at university. It seems a shame to leave it laying around on a hard drive, so I’m going to post it here.
This post provides an overview and summary of quantum cryptography. It contains explanations of how and which parts of quantum mechanics are used and a compares with classical cryptography. It covers quantum key distribution, which is commercially available, the quantum key distribution protocols including BB84, and quantum repeater networks. It is found that quantum cryptography is advancing and that even if full quantum communication is not realisable, the quantum protocols and methods are able to add security to existing cryptographic techniques.
I. INTRODUCTION
Quantum cryptography is potentially the next major stage in encryption. It is both necessary and desirable to be able to send messages privately, just as it is desirable to unauthorized parties to be able to intercept or decrypt these messages. This on-going battle ensures constant advancements in the field [23]. This paper will use the well-established identifiers of Alice, Bob and Eve when considering the different parties involved in an encrypted communication. Alice and Bob are the two parties communicating privately whilst Eve is the eavesdropper, occasionally with malicious intent.
Classical cryptography is based on the difficulty of computationally hard problems, most of these centre around the factorisation of large prime numbers. This makes them computationally secure, i.e. infeasible to brute force with modern technology and techniques [23].
As stated by Kerckhoff in 1883, a good encryption algorithm is one that can be known by the enemy yet leave the plaintext message secure to any attempts at decryption besides using the (secret) key [15]. Modern algorithms such as RSA and Diffie-Hellman are public knowledge and still secure. They are however only secure because an adversary will not have the computational resources to break the encryption in a reasonable time. With the availability of instant, cheap and immense computing power for hire in the cloud, these methods of encryption could be approaching a limit, and certainly will be inadequate once quantum computers are available and capable of running specified algorithms [23].
An information-theoretically secure algorithm will be unconditionally secure and have been derived using information theory. As such even a computationally advanced attacker cannot break the encryption of a message, as there simply is not enough information available. A notable example of such an implementation is the one-time pad. A message send using a one-time pad has no fixed key to crack, and no details of the encryption are communicated over the channel – the most an attacker can deduce is the maximum length of the plaintext.
For one-time pads to be used, each party must have a copy, much like a shared key. Any security offered by a one-time pad is lost if a part of it is reused, thus it must have a length greater than that of the sum of messages sent using it, and a random number generator (RNG) incapable of generating repeat or predictable output [15]. This has made it difficult to implement in the real world. Many implementations of cryptographically secure (pseudo-)random number generators exist (CSPRNG) exist and are suitable for this purpose. Hardware components are a common addition as it expands the randomness beyond code into the environment, and so hopefully making it less predictable.
The pad will also run out unless it can be frequently appended to – something that requires communicating the new material to the second party. This introduces the risk of observation, making the new material unsafe to use. Fairly obviously, but worth stating is that nothing would be gained by using up pad content to transmit more pad content, as it would lead to an overall loss in remaining pad.
II. QUANTUM CRYPTOGRAPHY
Quantum mechanics can offer a solution here. The Heisenberg uncertainty principle states that due to the linked nature of the properties of a quantum particle, it is fundamentally impossible to measure the state of one without altering it. This can be exploited to provide a communication system in which a message can only be received correctly once [2]. In this way the presence of an eavesdropper can be detected immediately.
Detection of eavesdropping in classical communication is overall impossible as packets and bits can be duplicated with little to no latency or need for specialised equipment. Although this does not necessarily infer that the security of the communication has been compromised.
Quantum Key Distribution
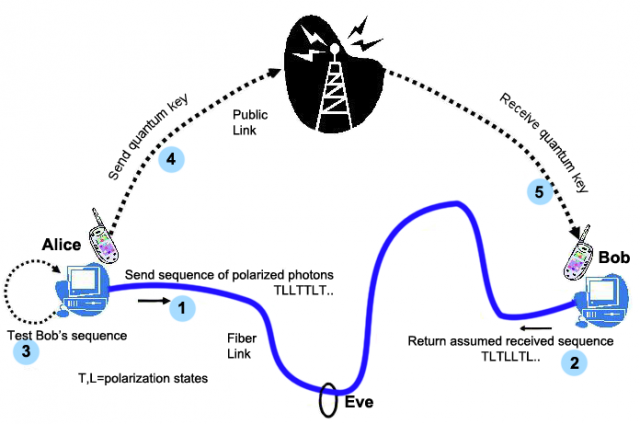
Quantum key distribution is the most developed area of quantum cryptography. The behaviour provided by quantum mechanics joined with an algorithm or protocol, allows Alice and Bob to construct a shared key in full view of Eve, but without her being able to capture or deduce it.
Communication using quantum bits is as yet un-developed due to the inherent uncertainty. This means that a particular key cannot be chosen in advance. It is also the reason why any actual communication must still occur on a classical channel.
As mentioned previously messages encrypted using a one-time pad are impossible to crack if it is used correctly. Alice and Bob therefore require a second channel of communication by which they can fill the pad. In the most extreme case this could be on an encrypted hard drive in a guarded briefcase, and in a more common case this would be through some information transmitted through an already established and encrypted channel, although of unknown secureness. A quantum channel offers an alternative [5].
In classical cryptography and networks, the entire exchange can be monitored and copied by Eve, although this will not necessarily provide access to the plaintext payloads. If Eve controls or has access to a portion of the network, she can completely passively duplicate the packets. She can then keep that copy to break at her leisure.
Man-in-the-middle (MITM) attacks are unavoidable in communication over any network infrastructure which can be accessed by Eve. In this case Eve will intercept communications and pretend to Alice that she is Bob, and to Bob that she is Alice.
Pre-shared public keys are commonly used to identify the other party in a connection and make MITM attacks harder to pull off. These keys are hosted by a trusted third party. A MITM cannot successfully exist without persuading both parties to use its own public key for encryption.
The weakest part of an exchange using classical cryptographic methods is the key exchange; if this is compromised Alice and Bob will be unaware and continue to use the presumed secret key for their private communication. An example of this in practice is determining the shared key used by a device to connect via Wi-Fi to an access point. The breaking of the key itself is a brute force operation, which is only made possible by capturing the initial handshake (key exchange) phase between the two devices.
Classical methods can be used securely after the secret key is exchanged using quantum methods, evading eavesdropping and allowing the use of existing infrastructure and algorithms.
III. KEY DISTRIBUTION PROTOCOLS
Purely sending a stream of quantum particles is not enough to create a secret shared key. Whilst this suitably results in the knowledge that a third party does not know the key, it means that neither Alice nor Bob have a shared key which can be used.
A series of protocols starting with BB84 deliver possible methods for turning this into a useful and secure key. The quantum particles used tend to be photons.
A. BB84
BB84 was the first protocol; variations on it still hold the top positions when considerations of protocols are made. It was defined by Bennett and Brassard in 1984, and makes use of the polarization property of photons [2].
As with all quantum protocols an eavesdropper cannot observe the communication without disturbing it. This disturbance, due to the unknown nature of quantum states, cannot be rectified before the communication is sent on to the intended recipient, regardless of how much time is taken by Eve.
A polarized photon is obtained by polarizing a beam of light using traditional polarizing filters or crystals, and then retrieving a single photon from within that [2].
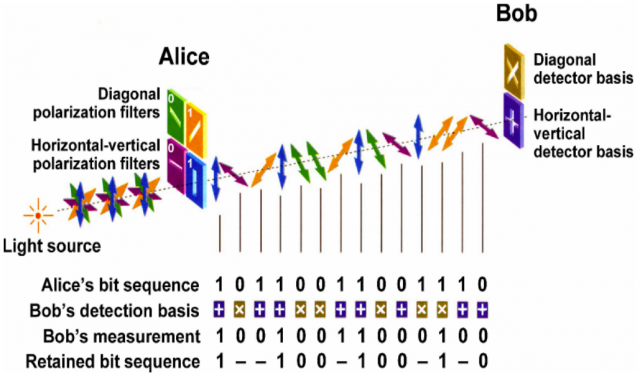
In BB84 there are 4 possible directions of polarization, two pairs of orthogonal states, represented by the angles 0 and 45 degrees, which correspond to a binary value of 1, and inversely 90 and 135 corresponding to a binary 0. Figure 2 displays these. Although not used in the original BB84, there also exists circular polarization, providing an increased number of directions.
Alice generates a bit using some CSPRNG, this will be a 1 or a 0. She then randomly selects one of the two polarization directions (basis) that could represent that bit value and then uses it to transmit with. This polarization will become part of the photon’s wave function. Alice will store the values she chose before repeating enough times to generate a suitably long string of quantum bits.
Each time Bob receives a photon he must decide upon a basis in which to measure it. Bob cannot base this decision on anything, and so it is a random choice out of the two bases.
When read with the correct angle, the photon survives as is. When read with a perpendicular angle, the photon is absorbed completely. When read with any other angle only a subset of the photons pass through and will be polarized in the direction of the used filter, destroying any information of the prior direction [2]. Regardless of the outcomes, Bob will log all information.
The correctness of the guessed bases can be discussed publicly without revealing the bits, Eve has already missed them. If she had read them, Bob would not have received them. The basis comparison allows the recipient to know which of the bits were received with the correct filter, and thus which to trust. The original string of bits will have been reduced to about half by this point.
To stop a MITM being able to manipulate the key by setting the same base for all bits and so knowing what it is, a subset of those received by Bob, roughly a third, are then announced publically over the classical channel for confirmation. If a particular limit is reached for incorrectness, then the presence of Eve is assumed and the key dropped in favour of beginning again.
Assuming confidence that the channel was not manipulated, the key to be used for further secure communication is built from the remaining, un-announced correct bits. This key will be much shorter than the original bit sequence [2] and as such will require a long starting string from Alice [21].
Eve will have trouble performing a MITM attack due to the escalation of incorrect bits caused by incorrect interceptions by both her and Bob. She cannot miss any photons in the retransmission phase as they are sequentially numbered, so must guess at what the photon she failed to measure was [5].
B. B92
Bennet proposed a minor change to the BB84 protocol in 1992. He suggested reducing the number of polarized states from four to two. The intended benefit was that the recipient could not obtain an incorrect bit on incorrect polarization measurement, but would instead receive an inconclusive result [5].
This cut down on the wastage of the bits used for checking correct decoding, and saves the extra time spent communicating over the public channel. If a definite result is obtained, then it is correct [11].
In this case a MITM could intercept all of Alice’s photons, and only send replacements for those she was able to guess correctly. This would leave Bob and Alice with the same correct bits. This results in a severe decrease in transmission rate to Bob. Alice can overcome this by sending a separate ‘decoy’ pulse in parallel. It is therefore less efficient than BB84 but is a more practical implementation [5, 12].
The problem faced by these protocols is that they use single photons. Obtaining single photons is difficult. Attempts to produce one can either result in no photon, or multiple photons.
In the case of multiple photons, their trip through the polarization filters will leave two photons which are effectively the same. This is a large security risk as it provides a way around the security offered by the no-cloning theorem. The eavesdropper can detect and take the duplicate photon (which won’t be missed), she can then store this for decoding once the bases have been announced in the public channel [5, 21]. This is known as photon number splitting (PNS).
In 2011 Kartalopoulos [21] noted a lack of “off-the-shelf sources” for single photons. In early 2012 an article [17] showed a production device designed to reliably detect single photons at speed. Being able to detect single photons is a huge step towards making sure there is only one. However redirecting single photons from a stream at speed without losing any is still an issue. A potential solution is the use of Faraday mirrors [21].
C. SARG04
SARG04 was one attempt to improve upon on the BB84 protocol and strengthen its resilience against Eve’s PNS attacks [5, 25].
To ensure multiple photons were not released, strongly attenuated laser pulses were employed. These can be tuned such that the average probability of a photon existing in a pulse is less than one. Very occasionally a single photon will be emitted, but unfortunately most of the pulses will be void of any photons [25]. Figure 3 shows an implementation of SARG04.
Despite handling PNS attacks, SARG04 has been found vulnerable to other forms of attack.
Up to this point the protocols mentioned have been classed as ‘prepare and measure’. The algorithms behind them can however be ported to versions using on entanglement.
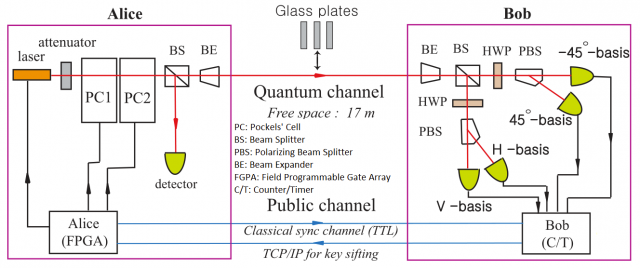
An implementation of the SARG04 protocol, showing a detailed view of quantum devices
Published in [25]
D. E91
Before the use of attenuated laser pulses, Ekert proposed the use of entanglement in the form of Bell states to overcome the problems of multiple photon sources [5].
A photon can be split into two entangled photons. Each will necessarily have a lower energy than the original photon. If one of the two photons is affected, the other will instantaneously be affected, regardless of distance between the two. The fundamental principles of quantum mechanics deny the use of this for instantaneous, faster-than-light communication.
Measuring with one part of a pair changes the state of the other, and if Eve was responsible, reveals her presence.
The effect of entanglement can be shown not to be predetermined at the point the photons are entangled, and that there is some form of instantaneous link through use of an experiment. One of the pair of entangled photons is polarized with a specific basis, whilst the other is left un-polarized. Upon testing the second photon’s polarization, it has been shown that it will always be at the orthogonal opposite to that of the first, regardless of the direction chosen for the photon that is polarized.
Entanglement can be added in to many classical protocols, giving them some of the benefits of quantum protocols [5].
With Ekert’s system , both Alice and Bob receive one each of each pair of entangled photons from a single source which takes and handles the splitting the photons into entangled pairs. The source can be controlled by Alice, Bob, or a third party, potentially even Eve.
The benefit of a single source over each party having to generate their own photons is largely cost, either monetary or maintenance and security. It is also the more likely situation in practice [9].
[9] also discusses the security of an untrusted source, specifically one that is controlled by Eve. The ability to actively detect that it is being manipulated it is said to be impractical as real-world hardware implementations will be imperfect. Conversely, a passive method of detection, utilizing an imperfect detector is found to work.
These three-party systems reduce the number of quantum devices required, which are expensive [24]. Yet without Alice and Bob holding their own quantum devices, they cannot detect tampering, requiring them to trust the source [10].
IV. QUANTUM NETWORKS
Although two entangled photons can affect each other from any distance, getting them that far away has issues. A large scale quantum network will require the signal to be boosted at times in order to allow the state to reach the destination. However a low energy photon cannot just be read and a new one emitted in its place due to it having a necessarily unknown state and doing such violates the no-cloning theorem [2].
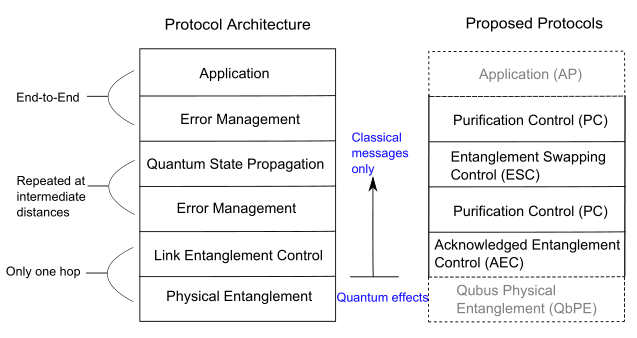
A protocol for a quantum network is described in [8] and shown in Figure 4. It aims to provide the same levels and abilities as a classical network. This includes the ability to buffer photons for delayed delivery, or rerouting. The quantum state of a photon can be propagated through entanglement swapping and quantum teleportation, in which two Bell pairs are spliced together. Pairs used for splicing have to be of high fidelity, in order to predict fidelity of a pair, a similar pair has to be destroyed in measurement [8]. There is no absolute certainty that the photon will remain of the same state having gone through this and although agreeing that some form of boosting is required [21] notes that there should be absolutely no interruptions in the photon’s path. This alone is unrealistic for any large scale network as it would require a mesh composition where every device is connected to every other. However a repeater network could lead to security issues if a photon can be read and then restored to its prior state [21].
Multiplexing communications in a single fibre could prove difficult thus making the system inefficient. Delays in arrival of photons could cause timing problems [21]. In classical networks multiplexing not only increases throughput, but adds to the security of the connection as it makes results from analysis less conclusive.
Long distance communication is achieved through optical fibres, although this a far too lossy medium for individual polarized photons – as there is only one, any leakage or interference can result in the photon not reaching its destination. As an alternative there is phase shifting but this is difficult to sustain. Finally there are entangled pairs, which can travel further than the photon they originated from [21], especially when coupled with teleportation and swapping.
Some work is being performed on long distance free-space links, in which photons are transmitted through the air using existing technologies such as infrared. One benefit of not being tied to using fibres is portability. [7].
Much work would need to be done to create a secure optical quantum network to rival the internet. Large sections of fibre would be exposed to untrusted locations in which they could be tapped with ease [12].
Fibres also leak, which would become an issue with individual photons, especially if the photons are leaked into an adjacent fibre. Current optical networks use out-of-band data for routing, which could be at risk of modification [12].
Methods in use to direct the flow of optical traffic introduce security problems, potentially allowing malicious users to control or deny access to parts of the network [12]. Although combatting denial of access attacks is harder than ensuring data is not manipulated or used in intercept-resent attacks.
Methods for securing protocols over networks are found in [12]. This entails both the privacy of information on the network, and the physical operation of the hardware.
An actual quantum network has been built linking Harvard and Boston universities with BBN Technologies, a company that has worked for DARPA on numerous occasions. The network is fully quantum with all authentication handled by quantum cryptography [23].
V. OTHER AREAS OF QUANTUM CRYPTOGRAPHY
A. Protocol Extensions
Various improvements can be made to the protocols. For instance, noise in the transmission is attributed to the presence of Eve as there is little way to be sure it is pure environmental noise or loss of photons due to imperfect hardware [5]. As a result of this and PNS attacks, a technique to create a key even when Eve holds some of the secret information has been created.
Devised by Bennett and Brassard, a technique known as ‘distilling’ or ‘privacy amplification’ can be used. The aim is to form a shared key that cannot possibly be known by Eve.
Uniformly distributed bits are taken from the key obtained with the protocol and universal hashing is used to form a key that cannot possibly be known by the eavesdropper [4]. The received bits are fed into a one way function to produce a new key of a shorter length, based on how many bits are deemed to have been compromised. This method can reduce the number of wasted key exchanges as much less information is needed to be kept secret [4].
Dense coding is a technique for sending two classical bits within one entangled pair. One is achieved through the entanglement effect, the other through photon transmission [10]. Alice and Bob each have one half of a pair of entangled photons, Alice can manipulate her photon, and in so doing cause a change of state in Bob’s. She can then also send her own photon to Bob, resulting in two bits using a single pair, and a single transmission.
Dense coding can also be used as an effective attack on quantum key distribution protocols when used with a three-party, single source set-up due to Alice and Bob being unable to detect interference. In a similar manner to a MITM attack, Eve intercepts all transmissions, replacing them with their own. They are able to determine and set correct states [10].
Fortunately defences against these attacks exist. Either Alice or Bob must shuffle the bits they send out or receive, so that the malicious party is unable to know which pairs they form parts of. This is an effective solution as it adds little overhead [10].
B. Quantum Computers
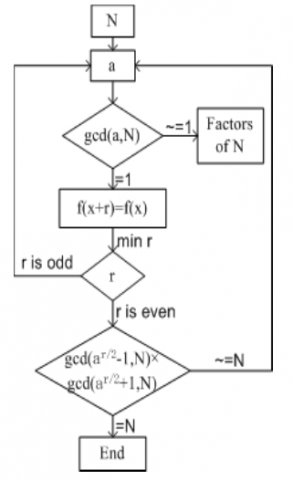 Shor’s algorithm is designed to do this, but it can only run on a quantum computer due to the use of quantum Fourier transforms. Similar algorithms such as the general number field sieve can achieve the same result on classical computers but will take much longer. The quantum version runs in polynomial time, whereas the classic can only manage sub-exponential. The quantum computer is used to simultaneously calculate every value of a function [27].The security of most encryption relies on the current difficulty of factoring large prime numbers. A quantum computer is theorized to be able to do this in a fraction of the time, rendering many common encryption techniques insecure.
Shor’s algorithm is designed to do this, but it can only run on a quantum computer due to the use of quantum Fourier transforms. Similar algorithms such as the general number field sieve can achieve the same result on classical computers but will take much longer. The quantum version runs in polynomial time, whereas the classic can only manage sub-exponential. The quantum computer is used to simultaneously calculate every value of a function [27].The security of most encryption relies on the current difficulty of factoring large prime numbers. A quantum computer is theorized to be able to do this in a fraction of the time, rendering many common encryption techniques insecure.
Figure 5 is Shor’s algorithm. ‘N’ is the publicly advertised product of two primes and ‘a’ is a randomly chosen number with a value less than N.
Some classical algorithms can resist attack by quantum computer. McEliece’s algorithm is based on an NP-hard problem, randomization, and Goppa codes. Until the recent discovery that it could resist Shor’s algorithm, it was left largely unused due to the need to share large matrices as overhead. It may now see an increase in use, especially with the high capacity channels now available.
C. Quantum Commitment
In cryptography commitment is the ability to set a value, without exposing it, for later reveal. This value can be proven to have not changed from the time it was set to the time it was revealed. For instance writing a number on a piece of paper and locking it in a briefcase which is then left in full view of all parties.
This has many uses, generally it is used in a manner in which Alice can prove to Bob that she knows something without revealing the details.
Unfortunately it is impossible to create such states with quantum particles and have them stay secure [28].
CONCLUSION
Numerous classical cryptographic algorithms are based on computational hardness, which whilst still a long way from being feasible to compute, is not going to hold up forever. Quantum cryptography can provide enhancements to the classic protocols, by adding the ability to detect eavesdroppers, even though complete quantum information exchange is not possible yet.
Whichever protocol is used for quantum cryptography, the quantum channel can provide a constant stream of secret random bits shared between Alice and Bob rather than stopping after enough exist to use as a shared session key. The constant stream of bits is then effectively a one-time pad, and can be used to encrypt the messages on the classical channel.
Quantum communication is not immune to all attacks, if Eve successfully blocks a quantum channel forming between Alice and Bob, they may be forced to fall back on a less secure protocol to Eve’s advantage [21], although this is true of classical systems too.
Quantum key distribution is the only part of quantum cryptography to have hardware is commercially available 1,2,3,4 [23, 26]. This is a good sign for the future of it as a future stage of communication. Although as pointed out in [24] porting classical ideas to quantum networks is difficult, and useful technologies such as signatures and public keys will require quantum alternatives before a quantum system can exist as a main method of communication without use of secondary classical channels.
Actual implementations of designs which are theoretically unconditionally secure can suffer from implementation and environment issues such as lost photons, noise, and physical manipulation and become vulnerable to attack. Some commercially available systems have been found vulnerable in the past [24], but this will improve with time.
1 http://swissquantum.idquantique.com/?-Quantum-Cryptography-#q4
2 http://www.idquantique.com/scientific-instrumentation/clavis2-qkd-platform.html
3 http://magiqtech.com/MagiQ/Products.html
4 http://qlabsusa.com/technology/cryptography/quantum-cryptography/
REFERENCES
[1] C.H. Bennett, G. Brassard, S. Breidbart, S. Wiesner, “Quantum cryptography, or unforgeable subway tokens”, in Advances in Cryptology: Proceedings of Crypto, 1982, New York: Plenum, pp. 267-275
[2] C.H. Bennett and G. Brassard, “Quantum Cryptography: Public key distribution and coin tossing”, in Proceedings of the IEEE International Conference on Computers, Systems, and Signal Processing, Bangalore, Dec 1984, pp. 175-179
[3] I. Devetak, “The Private Classical Capacity and Quantum Capacity of a Quantum Channel”, in Information Theory, IEEE Transactions on, Jan 2005, IEEE, vol. 51, pp. 44-55
[4] C.H. Bennett, G. Brassard, C. Crepeau, U.M. Maurer, “Generalized Privacy Amplification”, in Information Theory, IEEE Transactions on, Nov 1995, IEEE, vol. 41, pp. 1915-1923
[5] M. Javed, “A survey of quantum key distribution protocols”, in Proceedings of the 7th International Conference on Frontiers of Information Technology, 2009, ACM
[6] F. Vatta, R. Romano, M.T.D. Alizo, “Turbo codes for Quantum Key Distribution (QKD) applications”, in Proceedings of the 4th International Symposium on Applied Sciences in Biomedical and Communication Technologies, 2011, ACM
[7] R. Corvaja et al, “Engineering a Long Distance Free-Space Quantum Channel”, in Proceedings of the 4th International Symposium on Applied Sciences in Biomedical and Communication Technologies, 2011, ACM
[8] L. Aparicio, R.V. Meter, H. Esaki, “Protocol Design for Quantum Repeater Networks”, in Proceedings of the 7th Asian Internet Engineering Conference, 2011, ACM
[9] X. Peng, H. Guo, “Source monitor in quantum key distribution”, in General Assembly and Scientific Symposium, Aug 2011, IEEE, pp. 1-4
[10] F. Gao, S.Qin, F. Guo, Q. Wen, “Dense-Coding Attack on Three-Party Quantum Key Distribution Protocols”, in Quantum Electronics,Journal of, May 2011, IEEE, vol. 47, issue 5, pp. 630-635
[11] V.L. Kurochkin, A.V. Rzhanov, “Protocols for Quantum Cryptography”, in Micro/Nanotechnologies and Electron Devices (EDM), 2011 International Conference and Seminar of Young Specialists on, Jul 2011, IEEE, pp. 114-115
[12] K. Kitayama et al, “Security in Photonic Networks: Threats and Security Enhancement”, in Lightwave Technology, Journal of, Nov 2011, IEEE, vol. 29, issue 21, pp. 3210-3222
[13] A. Chailloux, I. Kerenidis, “Optimal bounds for quantum bit commitment”, in Foundations of Computer Science, Annual Symposium on, Oct 2011, IEEE, pp. 354-362
[14] C. Antonelli, M. Brodsky, M. Shtaif, “Distance limitations on the entanglement distribution over optical fiber due to chromatic and polarization mode dispersion”, in Lasers and Electro-Optics, 2011 Conference on, May 2011, pp. 1-2
[15] M. Stipcevic, “Quantum random number generators and their use in cryptography”, in MIPRO, 2011 Proceedings of the 34th International Convention, May 2011, IEEE, pp. 1474-1479
[16] J. Mora, A. Ruiz-Alba, W.Amaya, J. Capmany, “Dispersion Supported BB84 Quantum Key Distribution Using Phase Modulated Light”, in Photonics Journal, Jun 2011, IEEE, vol. 3, issue 3, pp. 433-440
[17] H. Dyball, “1 GHz and counting”, in Electronics Letters, Jan 2012, IEEE, vol. 48, issue 2, p. 55
[18] R. Goel, M. Garuba, A. Girma, “Research Directions in Quantum Cryptography”, in Information Technology, Fourth International Conference on, Apr 2007, IEEE, pp. 779-784
[19] A. Sharma, V. Ojha, S.K. Lenka, “Security of Entanglement Based Version of BB84 protocol for Quantum Cryptography”, in Computer Science and Information Technology, 3rd International Conference on, Jul 2010, IEEE, vol. 9, pp. 615-619
[20] M.S. Sharbaf, “Quantum Cryptography: An Emerging Technology in Network Security”, in Technologies for Homeland Security, International Conference on, Nov 2011, IEEE, pp. 13-19
[21] S.V. Kartalopoulos, “Identifying vulnerabilities of quantum cryptography in secure optical data transport”, in Military Communications Conference, Oct 2005, IEEE, vol. 5, pp. 2788-2796
[22] A. Falahati, H. Meshgi, “Using Quantum Cryptography for securing Wireless LAN networks”, in International Conference on Signal Processing Systems, May 2009, IEEE, pp. 698-701
[23] M.S. Sharbaf, “Quantum Cryptography: A New Generation of Information Technology Security System”, in Information Technology: New Generations, Sixth International Conference on, Apr 2009, IEEE, pp. 1644-1648
[24] R.S. Vignesh, S. Sudharssun, K.J.J. Kumar, “Limitations of Quantum & The Versatility of Classical Cryptography: A Comparative Study”, in Environmental and Computer Science, Second International Conference on, Dec 2009, IEEE, pp. 333-337
[25] K. Hong, Y. Kim, Y. Kim, “Weak-pulse implementation of SARG04 quantum cryptography protocol in free space”, in 2008 Conference on Quantum Electronics and Laser Science, May 2008, IEEE, pp.1-2
[26] N. Jain, “Inducing a detector efficiency mismatch to hack a commercial quantum key distribution system”, in 12th European Quantum Electronics Conference on Lasers and Electro-Optics Europe, May 2011, IEEE, p. 1
[27] W. Zhang, C. Xu, F. Li, J. Feng, “A Period-Finding Method for Shor’s Algorithm”, in International Conference on Computational Intelligence and Security, Dec 2007, IEEE, pp. 778-780
[28] G. Brassard, C. Crépeau, D. Mayers, L. Salvail, “A brief review on the impossibility of quantum bit commitment”, Dec 1997, arXiv, at http://arxiv.org/abs/quant-ph/9712023 (link valid May 2012)